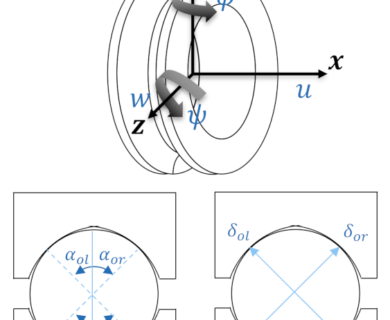
BB20 est un code de calcul analytique destiné à prévoir le comportement quasi-statique et quasi-dynamique des roulements à billes à 2, 3 ou 4 points de contact. BB20 est co-développé avec Safran AE et le LaMCoS de l’INSA Lyon.
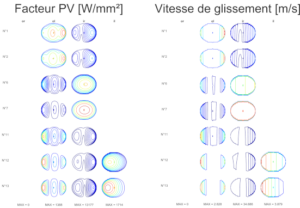
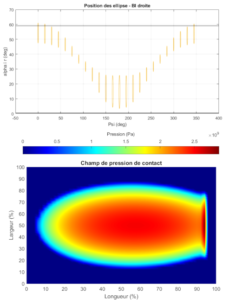
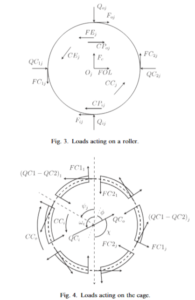
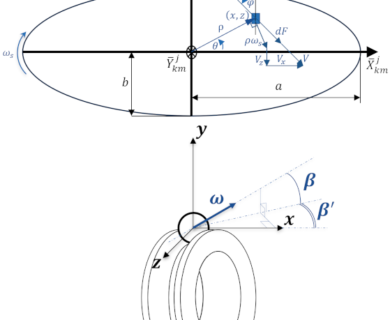
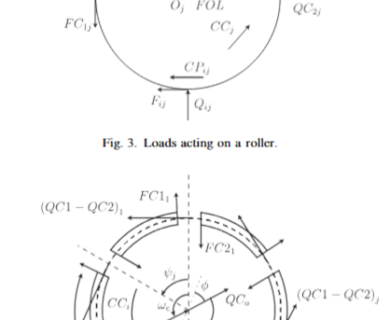
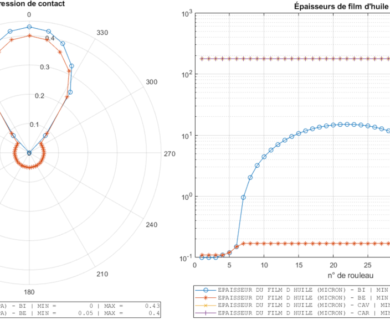
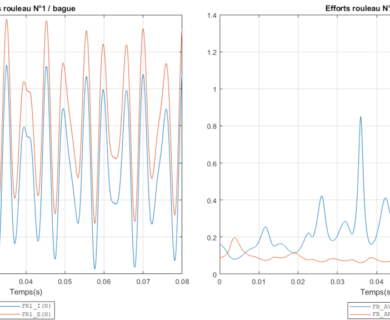
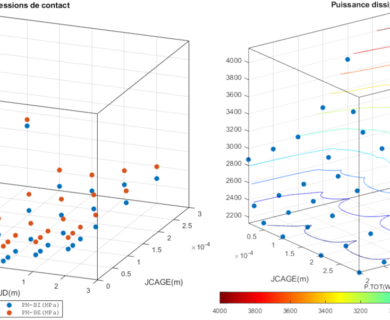
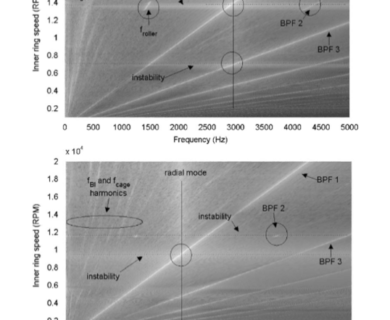
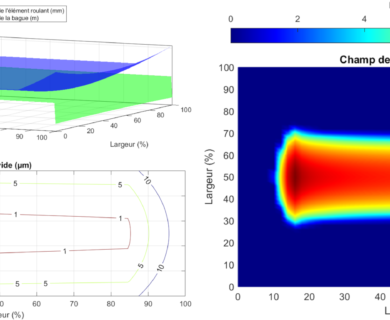
DYNAR est un code de calcul analytique destiné à prévoir le comportement quasi-statique et dynamique des roulements à rouleaux cylindriques. DYNAR est co-développé avec Safran AE et le LaMCoS de l’INSA Lyon.
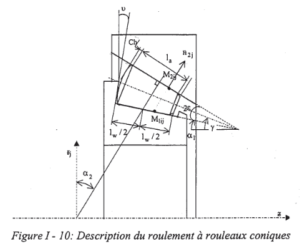
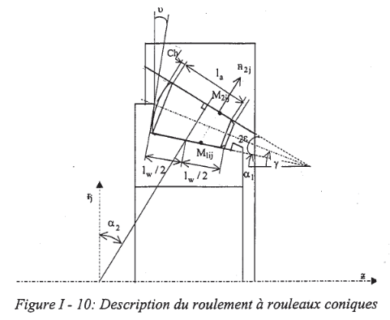
Additionnellement, Mecalam dispose de modèles simplifiés de roulements à billes et à rouleaux coniques et cylindriques destinés à intégrer des modèles de systèmes complets.