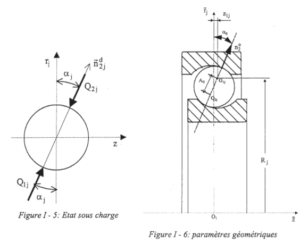
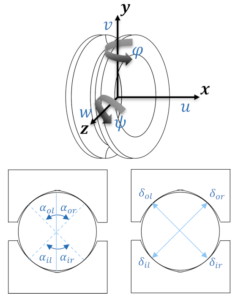
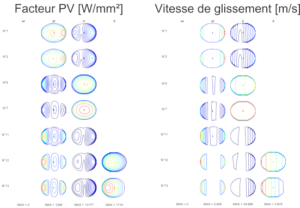
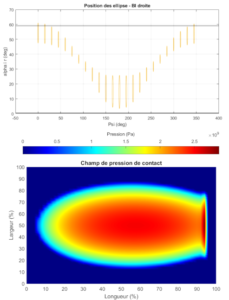
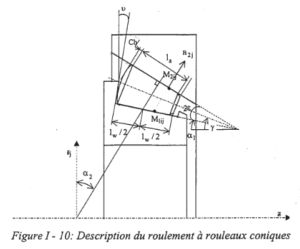
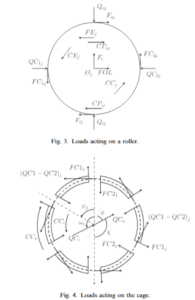
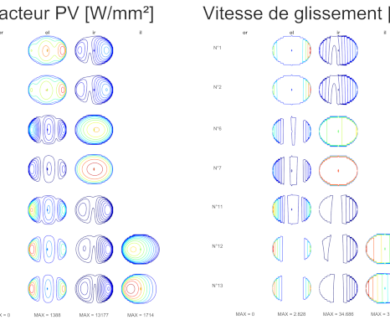
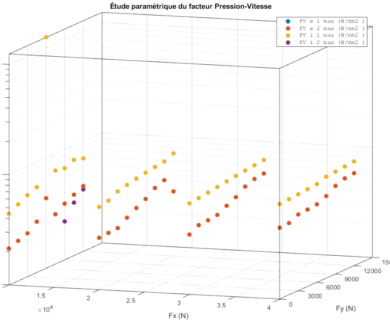
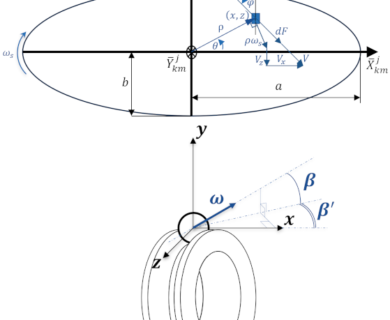
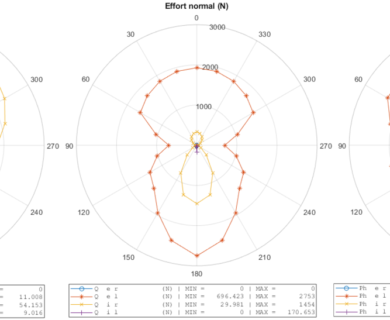
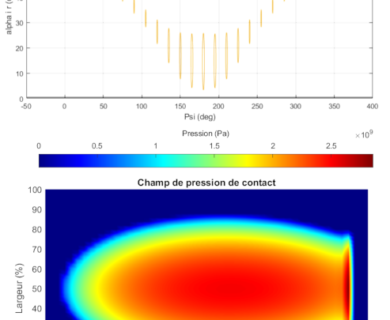
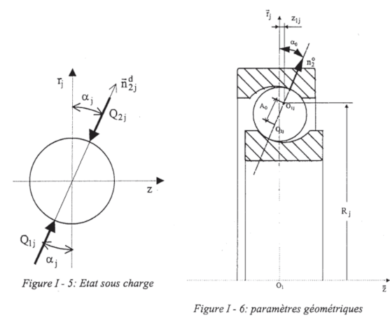
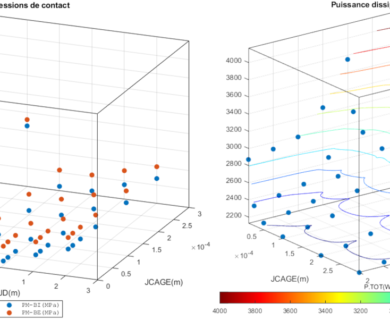
BB20 is an analytical calculation code designed to predict the quasi-static and quasi-dynamic behaviour of ball bearings with 2, 3 or 4 points of contact. BB20 is co-developed with Safran AE and the LaMCoS at INSA Lyon.
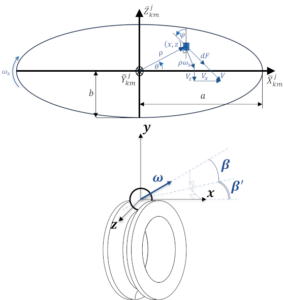
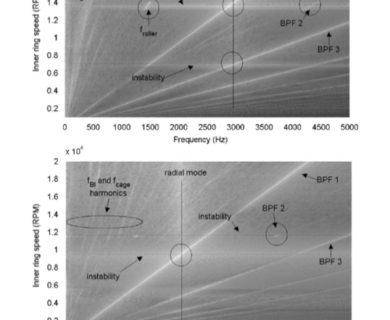
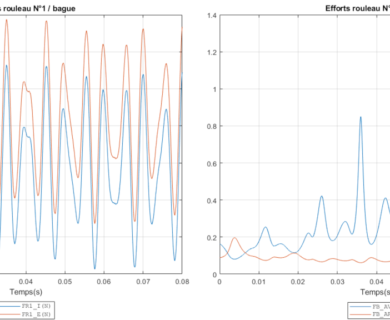
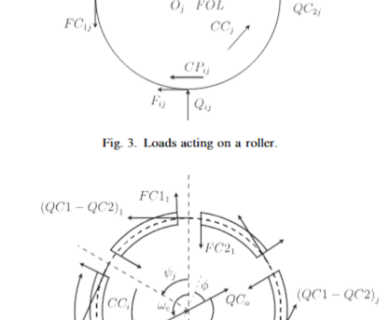
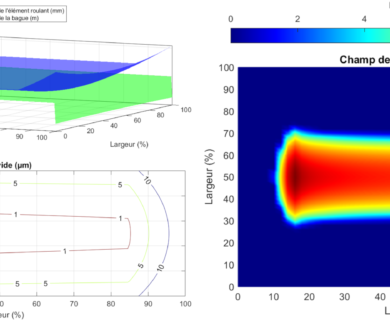
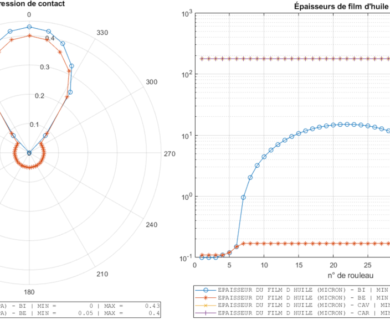
DYNAR is an analytical calculation code designed to predict the quasi-static and dynamic behaviour of cylindrical roller bearings. DYNAR eis co-developed with Safran AE and the LaMCoS at INSA Lyon.
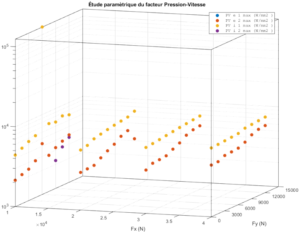
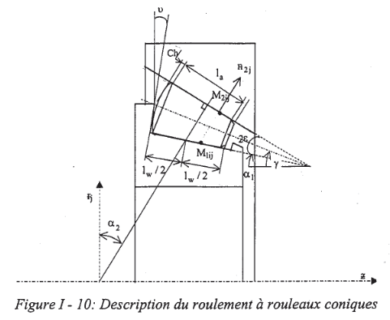
In addition, Mecalam has simplified models of ball, tapered and cylindrical roller bearings designed to be integrated into larger models of complete systems.